Simple Attractors

Published on 26 May 2008

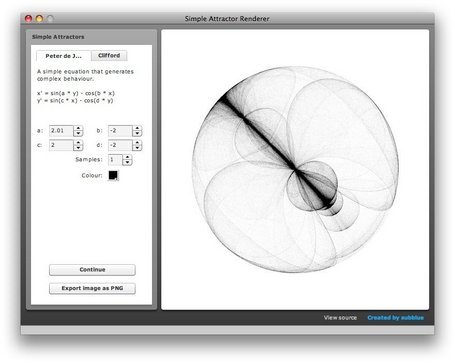
This little experiment lets you visually explore two very simple attractor equations that generate very unexpected and aesthetically pleasing results.

It was coded in Actionscript 3.0 and wrapped into an Adobe Air application so that you can export the rendered imaged as PNGs.

The two simple attractor equations are credited to Peter de Jong:

x' = sin(a * y) - cos(b * x)
y' = sin(c * x) - cos(d * y)

And Cliff Pickover:

x' = sin(a * y) + c * cos(a * x)
y' = sin(b * x) + d * cos(b * y)

Start with a random point x, y and plot a semi-transparent pixel at the calculated x', y' point. Plug the new x', y' values back into the equations to get the next point, and so on for a few hundred thousand iterations. Vary the a, b, c, d constants to give wildly different results.

View the gallery for more renderings.

Download the application and get the source code.
Note: you will need the Adobe Air runtime installed first.

  Last updated: 5 October 2008

3 Comments

• Gallery commented at 6 February 2009 at 19:14

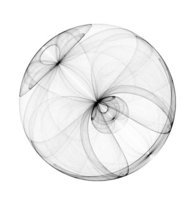
  I don't know why... but... man... The picture above makes me think about like... bottom of humans body... =\

• kpss sınavı commented at 16 December 2009 at 16:10

  it's very interesting. in fact easy to calculate, but it seems impossible at first. Thank you very much for your sharing. it will be very useful for me.

• Paul Web commented at 27 February 2012 at 02:09

  You never know what you are going to get when you add two attractor equations together. They might seem simple on their own, but by just adjusting the values on the points, we get to see some cool transformations. If Adobe Air the only program dedicated to seeing this? Or is there another program I can use?

Older: Harmonograph Newer: Nested semicircles