Mandelbrot

Published on 2 October 2008

Benoit Mandelbrot was the first person to study the function z′ = z²+c with a computer and the result is the iconic fractal shape that now takes his name.

Writing a script to render the Mandelbrot fractal has almost become a rite of passage for many programmers. Here is my version written in Actionscript 3.0.

Click/scrollwheel to zoom, shift + click to zoom out.
Command + drag or arrow keys to pan. m key to change mapping modes.
a to set anti-aliasing. f to go fullscreen. s to save out as a JPEG.
+ and - change the detail level - use when at a black boundary on a deep zoom.

The Mandelbrot formula z' = z² + c is calculated for each pixel where its coordinates seed the a and b components of the complex number c = a + bi. The output of the equation is fed back in as the new value of z and this is repeated until the magnitude of z' reaches a predefined bailout value. The number of iterations required to reach the bailout value is used to map a colour to the pixel. This is known as the "escape time" algorithm.

Mapping modes

Things start to get interesting when you play around with the mapping modes that convert the escape time to a colour. The standard mapping takes the escape time of the pixel as the index in an array of colour values. However, this approach results in colour banding around the fractal.

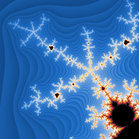The method used here is a continuous, smooth mapping known as the "normalised iteration count" algorithm. I've also added a variation to this called shelf mapping, which reverses the gradient for each colour band around the fractal and gives an interesting layered result.

There are a couple of additional variations of the shelf mapping which use different bailout conditions to produce either spiky or puffy results. Zoom in and it's like flying over an infinite forest of sea anemones!

The last mapping mode is binary decomposition, which although it sounds fancy is actually quite straight forward. If the angle between the real and imaginary parts of the final z is > 0 colour the pixel white otherwise colour it black.
You should enable the anti-aliasing option for best results with this mapping mode.

Performance

The default zoom factor for each click is 2x magnification, but you can only zoom to a maximum of around 8e12. This is due to the limited precision of the Number data type in Actionscript 3.0. Once you reach the limit you might see glitches due to rounding errors. It would be interesting to implement an arbitrary precision floating point data type in Actionscript, but the performance would probably make impractical for anything fractal related.

If you are using Flash 10 then you should notice quite a speed increase compared to Flash 9. There seem to have been quite a few performance tweaks made in this latest release.

Fractal Explorer

This demo is in effect a prototype for a full blown Flash fractal explorer I'm currently working on that will let you define colour palettes, different mapping modes and fractals types. Stay tuned for more fractal explorations!

Download the AS3 source and play with the Mandelbrot Explorer.

  Last updated: 5 October 2008

7 Comments

• Tom commented at 7 October 2008 at 22:36

  great job ! congrats

• Cyclone commented at 17 December 2008 at 21:38

  Astounding! I coded my first Mandelbrot a few months ago. Nice job with the smooth coloration! I used the "Escape Time Algorithm" for mine, couldn't figure out for the life of me how to do it like yours.

  The controls you added function very well. I will have to download your source to see how you did it!

  As a huge fan of fractals, I figured out a recursive algorithm for drawing a Sierpinski Gasket which greatly shortens the normal turtle-art approach. If you like, I can send a copy to you once I am done.

  Phenomenal job with the near realtime rendering!

• I, Gallery =) commented at 15 January 2009 at 19:41

  Aha. Seen such on Wiki.. =)

• jchook commented at 24 May 2009 at 03:49

  You should make a distributed computing buddhabrot generator. Users would be generating the next most detailed version of the buddhabrot while browsing the most recently completed version in a way similar to this website: http://gigapixelphotography.com/vancouver-yaletown-condos

• vijay shan commented at 15 July 2009 at 03:45

  great work the color selection is incredible.

• Fractalia commented at 26 March 2010 at 05:32

  Very nice job.
  Here is a similar work that also shows Julia and has the ability to set some parameters:
  http://www.ladimolnar.com/Fractalia/

• aldeol commented at 4 June 2010 at 23:55

  I really surprised. This science? or technology? The controls you added function very well. I will have to learn your source to see how you did it! thank you very much...

Older: Welcome to the new site Newer: Guilloché Patterns